跳至主要內容

数据结构中常见的树

moyusisiAlgorithm数据结构

经常见到的树有: BST二叉排序树, AVL平衡二叉树, B树, B-树, B+树, B*树, RBT红黑树

BST树

二叉排序树, 也称二叉查找树(Binary Search Tree), 简称BST.

定义

二叉排序树或者是一棵空树, 或者是一棵具有下列特性的非空二叉树:

  • 若左子树非空, 则左子树上所有结点关键字值均小于根结点的关键字值
  • 若右子树非空, 则右子树上所有结点关键字值均大于根结点的关键字值
  • 左右子树本身也分别是一颗二叉排序树

示例

下图中左右两个都是二叉排序树

BSTTree
BSTTree

二叉排序树的查找

从根结点开始进行关键字比较, 若相等, 则查找成功; 若不等, 如果查找的关键字小于根结点关键字, 去左子树中查找, 否则去右子树中查找. 若最后不再有子树, 查找失败.

二叉排序树的插入

与查找过程类似, 若待插入的BST树为空, 则直接插入; 若关键字k小于根结点关键字, 则插入到左子树, 否则插入到右子树

二叉排序树的删除

删除操作可以按下面情况处理

  1. 若被删结点z是叶子结点, 则直接删除, 不会破坏二叉排序树的性质
  2. 若z只有一颗子树, 则让z的子树成为z父节点的子树, 即替代z的位置
  3. 若z有左右两棵子树, 则令z的直接前驱(即z左子树中最大的那个结点)替代z, 再从左子树中删除这个直接前驱, 这样就转化成了第一或第二中情况(因为z的直接前驱, 肯定没有右子树)

AVL平衡二叉树

平衡二叉树的发明者为Georgy Adelson-Velsky和Evgenii Landis, 所以也被称作AVL树. 在维基百科AVL树的定义中有这么一句话: In computer science, an AVL tree is a self-balancing binary search tree., 所以AVL平衡二叉树是BST二叉搜索树的子集.

定义

平衡二叉树或者是一棵空树, 或者是一棵具有下列特性的非空二叉树:

  • 它的左右子树高度差绝对值不超过1
  • 它的左右子树都是平衡二叉树

虽然AVL平衡二叉树的定义中并没有体现它是一个排序树, 但它是以二叉排序树为前提的

平衡二叉树的插入

二叉排序树插入时, 只需要保证排序的特性, 平衡二叉树的插入同时还需要保证插入结点之后仍然平衡.
平衡二叉树的插入过程前半部分与二叉排序树相同, 但在新结点插入后, 如果破坏了某个结点的平衡, 则需要作出相应的调整. 一般可将失去平衡后进行调整的规律归纳为下列4种情况:

  • LL平衡旋转(右单旋转)。在结点A的左孩子(L)的左子树(L)上插入新结点, 导致以A为根的子树失去平衡, 此时需要做一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点, 将A结点向右下旋转成为B的右子树的根结点, 而B的原右子树则成为A的左子树。 过程如下图:
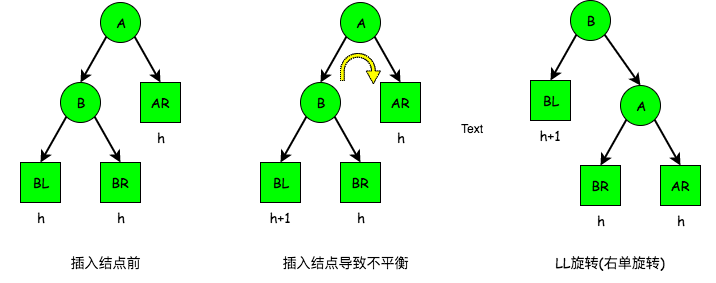
AVL_LL
AVL_LL
  • RR平衡旋转(左单旋转)。在结点A的右孩子(R)的右子树(R)上插入新结点, 导致以A为根的子树失去平衡, 此时需要做一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点, 将A结点向左下旋转成为B的左子树的根结点, 而B的原左子树则成为A的右子树。 过程如下图:
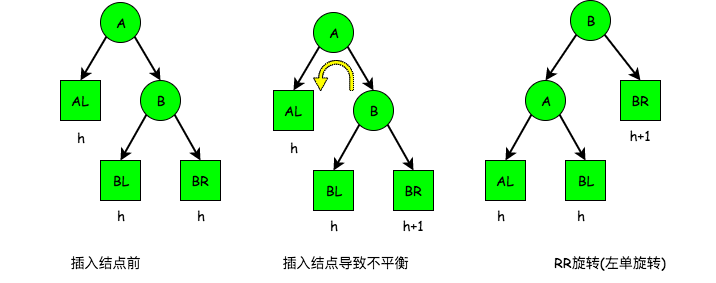
AVL_RR
AVL_RR
  • LR平衡旋转(先左后右双旋转)。在结点A的左孩子(L)的右子树(R)上插入新结点, 导致以A为根的子树失去平衡, 此时需要做两次旋转操作, 先左旋转后右旋转。将A的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置, 然后再把C结点向右上旋转提升到A结点的位置。 过程如下图:
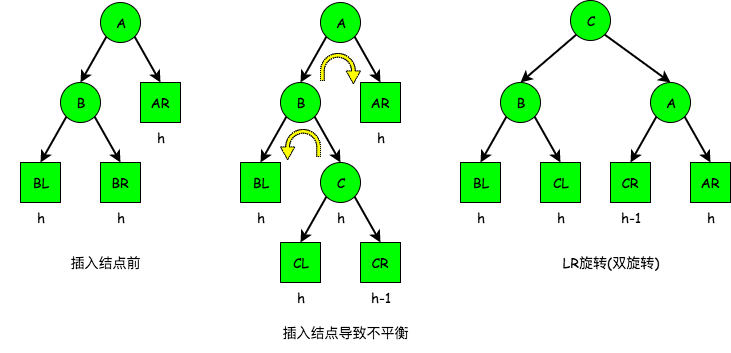
AVL_LR
AVL_LR
  • RL平衡旋转(先右后左双旋转)。在结点A的右孩子(R)的左子树(L)上插入新结点, 导致以A为根的子树失去平衡, 此时需要做两次旋转操作, 先右旋转后左旋转。将A的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置, 然后再把C结点向左上旋转提升到A结点的位置。 过程如下图:
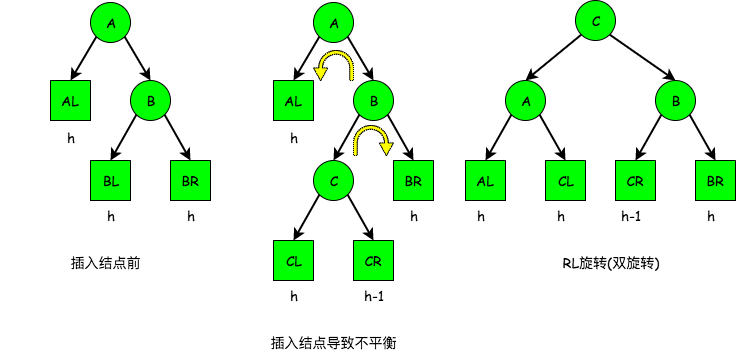
AVL_RL
AVL_RL
  • 注意, 在LR和RL旋转时, 究竟新结点插入在C的左子树还是右子树上, 不影响旋转过程。

平衡二叉树的删除

AVL的删除过程前半部分与BST相同, 但删除结点后, 如果破坏了父结点的平衡, 则需要作出相应的调整, 调整方法与插入时的调整方法一样

RBT红黑树

红黑树(Red Black Tree)也是一种二叉查找树, 但在每个结点上增加一个存储位表示结点的颜色(Red或Black), 通过对每个结点着色, 使它满足一些性质, 这些性质共同来保证红黑树是基本上平衡的.

AVL是严格平衡树, 因此在增加或者删除节点的时候, 根据不同情况, 旋转的次数比红黑树要多;
RBT是弱平衡的, 用非严格的平衡来换取增删节点时候旋转次数的降低;
所以简单说, 若搜索的次数远远大于插入和删除时, 选择AVL树; 若搜索、插入、删除次数几乎差不多, 应该选择红黑树

RBT的性质

红黑树是每个结点都带有颜色属性的二叉查找树。 此外, 对于任何有效的红黑树必须满足以下特点:

  1. 结点是红色或黑色
  2. 根结点是黑色
  3. 每个叶结点(空结点NULL)是黑色的
  4. 每个红色结点的两个子结点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色结点)
  5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点

这些特点共同限制了红黑树的关键性质: 从根到叶子的最长路径不多于最短路径的两倍长。这就保证了这个树大致上是平衡的。

  • 这些性质如何保证最长路径不多于最短路径的两倍长?

性质5保证根结点到叶结点的所有路径都有相同数目的黑色结点;
性质2和性质3保证最长路径(从根开始)两头都是黑色的;
性质4保证了路径不能有两个相连的红色结点, 最短路径都是黑色结点, 最长路径有交替的红色和黑色结点;
这就表明了没有路径能多于其他路径的两倍长

RBT示例

RBT
RBT

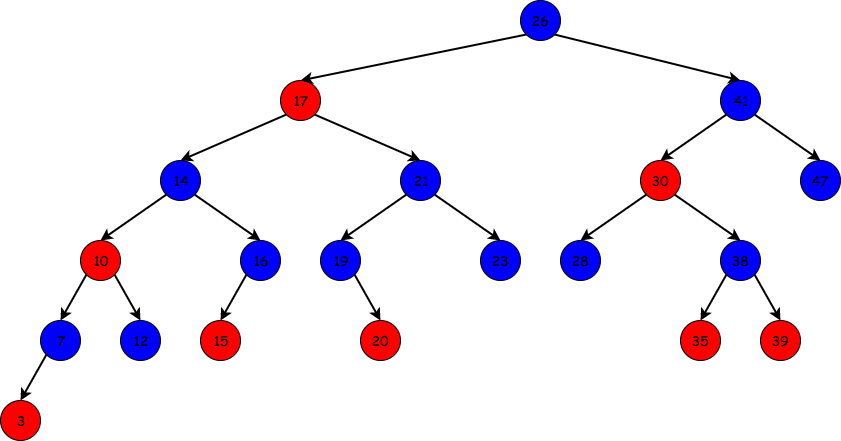
红黑树的插入

在对红黑树进行插入操作时, 我们一般总是插入 红色 的结点。因为插入黑结点会增加某条路径上黑结点的数目, 从而导致整棵树黑高度的不平衡。
当插入红色结点时, 如果插入的结点是根结点, 会破坏性质2; 如果插入结点的父结点是红色, 则会破坏性质4, 这时就需要对红黑树做一些调整。所有可能的情况有4种:

  • 情况1: 插入的是根结点(空树)。

此时违反性质2, 直接把新结点改成黑色即可。

  • 情况2: 插入的结点的父结点是黑色(黑父)。

此时不会违反任何性质, 红黑树没有被破坏。

  • 情况3: 父结点是红色(红父)。

若父结点为红色, 祖父结点必定为黑色, 否则就不是红黑树了。红父这种情况破坏了性质3, 需要调整, 需要根据叔父结点(祖父的另一个孩子)的颜色来决定做什么样的操作, 这又分两种情况

  • 3.1: 叔父结点为红色(红父红叔) 红父红叔这种情况, 如下图所示, 无需旋转, 只要将父和叔结点变为黑色, 将祖父结点变为红色即可。
    但由于祖父结点的父结点有可能为红色, 从而违反红黑树性质, 此时必须将祖父结点作为新的判定点继续向上进行平衡操作。
红父红叔
红父红叔

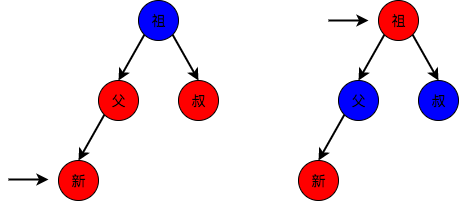
注意 这种情况, 无论红叔是在左边还是在右边, 操作都是一样的。

  • 3.2: 叔父结点为黑色(红父黑叔) 红父黑叔这种情况, 需要进行旋转, 有LL, LR, RR, RL等情况, 旋转方式与AVL类似。如图:
红父黑叔
红父黑叔

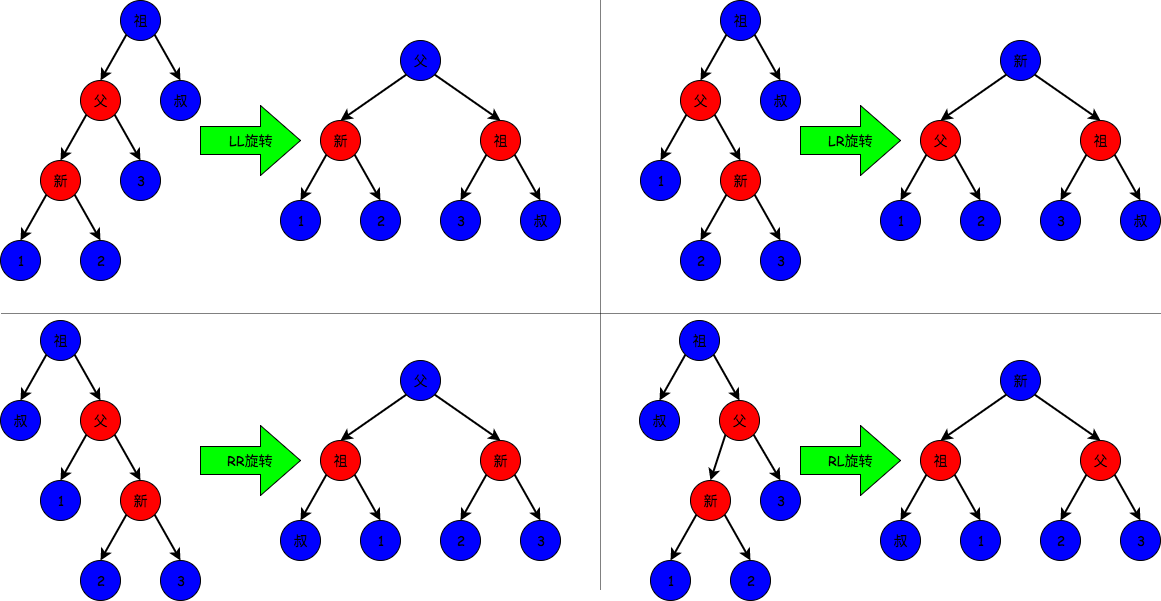
注意 当旋转完成后, 就已经是红黑树了, 此时不需要再向上调整; 上面四张图的叔、1、2、3结点有可能为黑哨兵(NULL)结点。

红黑树的删除

红黑树本身是一棵二叉查找树, 它的删除和二叉查找树的删除类似。根据前面BST的删除操作可知, 真正删除的结点要么没有子树(情况1), 要么只有一颗子树(情况2、3)。所以真正删除的结点 只有一个孩子 或 没有孩子。 再结合红黑树的特点, 可以得出以下两个结论:

  1. 真正被删除的必定是没有孩子的结点或只有一个红色孩子的结点
  2. 如果真正删除的结点是一个红色结点, 那么它必定是一个叶子结点

根据这两个重要结论, 删除操作有以下情况:(旧点表示真正要删除的结点, 新点表示旧结点的孩子结点)

  • 1.旧点为红色: 根据结论2, 若旧点(真正要删除的结点)为红色, 则它必是叶子结点, 这种情况直接删除即可.

  • 2.一红一黑: 若旧点为黑色, 新点为红色时, 新点取代旧点位置后, 将新点染黑即可

  • 3.双黑: 当旧点和新点都为黑色时(新点为NULL时, 也属于这种情况), 情况比较复杂, 需要根据旧点兄弟结点的颜色来决定进行什么样的操作, 兄弟结点又分红兄和黑兄两种情况。情况略复杂, 具体可以参考这篇文章

B树,B-树,B+树

B树又称多路平衡查找树或多路平衡查找树, 英文为B-Tree有的翻译成B树, 有的翻译为B-树, 两者是同一个东西.

关于B树和B+树, 查找算法中已有详细介绍.

上次编辑于:
贡献者: moyusisi
Copyright © 2025 moyusisi